Olympiad Report

PLACEMENT

Dear Parent,
Last month, Luke Ryan participated in the Online Challenge of the International Math Contest. Below you will find a report detailing Luke Ryan’s performance on the contest. We hope that this will give you deeper insight into Luke Ryan’s grasp of various mathematical concepts as compared to that of Luke Ryan’s international peers.

Please note that this analysis is based on a sampling of problems across several concepts, and Luke Ryan’s performance on each. Student performance can be impacted by a variety of factors including distractions while taking the test, level of tiredness, etc.

If your child has qualified for the International Math Contest Round 2, you will be notified in a separate email by end of March.

Congratulations on your child’s participation in the Online Challenge, and we hope to see you next year!

-RSM Foundation

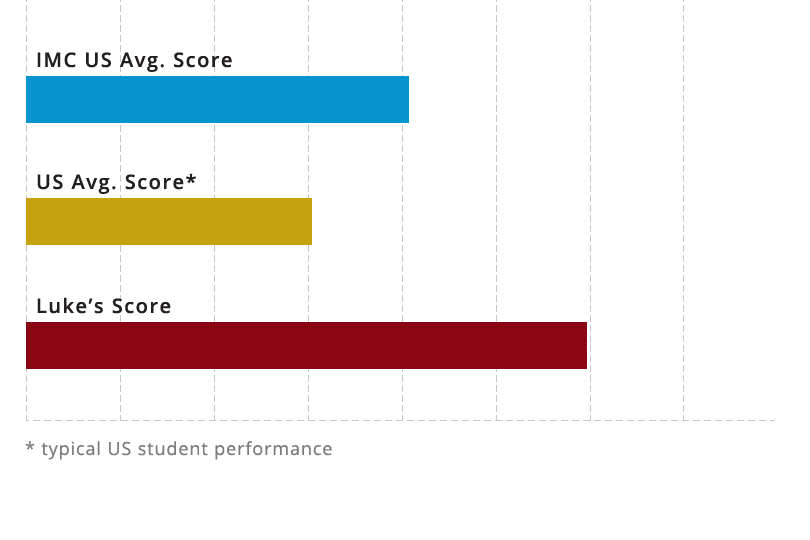
The Results are In

When compared to an international bar, your child is:

COMPETITIVE INTERNATIONALLY

PERCENTILE

Luke scored better than 80% of the participants in his grade.

PREVIOUS NEXT

RANKING

The contest problems covers concepts and skills typically mastered by Luke’s peers in countries renowned for high levels of achievement in mathematics education.

Luke’s performance indicates that his level of knowledge is on par with that of his peers in these countries.

PREVIOUS NEXT

STRENGTH AREAS

Proportional Reasoning: Ratios, Rates, and Percentages

Recognize proportional relationships; use ratios, rates, and percentages to solve problems.

Geometry

Apply definitions, formulas and theorems of Euclidean geometry to solve problems.

Problem Solving

Analyze problem situations, extract relevant details, and apply various strategies to find the solution to a problem.

GROWTH AREAS

Fractions and Decimals

Understand the meaning of a fraction and a decimal; perform operations with fractions and decimals.

Arithmetic: Operations and Properties

Use order of arithmetic operations and properties of these operations to compute efficiently; use algorithms for arithmetic operations.

PREVIOUS NEXT

ANSWERS

Luke Ryan correctly solved 9 problems of International Math Challenge for the 6th grade. He spent 30 minutes to complete the contest. View the full list of contest questions below.

Problem Number	Correct Answer	Provided Answer	% of Participants Solved this	Time Spent (min.)
1	42	42	94%	0.5
2	20	20	67%	0.5
3	61	61	83%	0.5
4	64	64	84%	1
5	29	29	70%	1
6	16	16	44%	1
7	144	144	51%	1
8	52	7	39%	3
9	210	210	37%	6
10	13	41	42%	3
11	18	18	15%	2
12	52	42	22%	9
13	329	452	14%	1
14	116	54	12%	2

Problem 1

Correct Answer	42
Provided Answer	42
See Solution
% of Participants Solved this	94%
Time Spent (min.)	0.5

See Less

Problem 2

Correct Answer	20
Provided Answer	20
See Solution
% of Participants Solved this	67%
Time Spent (min.)	0.5

See Less

Problem 3

Correct Answer	61
Provided Answer	61
See Solution
% of Participants Solved this	83%
Time Spent (min.)	0.5

See Less

Problem 4

Correct Answer	64
Provided Answer	64
See Solution
% of Participants Solved this	84%
Time Spent (min.)	1

See Less

Problem 5

Correct Answer	29
Provided Answer	29
See Solution
% of Participants Solved this	70%
Time Spent (min.)	1

See Less

Problem 6

Correct Answer	16
Provided Answer	16
See Solution
% of Participants Solved this	44%
Time Spent (min.)	1

See Less

Problem 7

Correct Answer	144
Provided Answer	144
See Solution
% of Participants Solved this	51%
Time Spent (min.)	1

See Less

Problem 8

Correct Answer	52
Provided Answer	7
See Solution
% of Participants Solved this	39%
Time Spent (min.)	3

See Less

Problem 9

Correct Answer	210
Provided Answer	210
See Solution
% of Participants Solved this	37%
Time Spent (min.)	6

See Less

Problem 10

Correct Answer	13
Provided Answer	41
See Solution
% of Participants Solved this	42%
Time Spent (min.)	3

See Less

Problem 11

Correct Answer	18
Provided Answer	18
See Solution
% of Participants Solved this	15%
Time Spent (min.)	2

See Less

Problem 12

Correct Answer	52
Provided Answer	42
See Solution
% of Participants Solved this	22%
Time Spent (min.)	9

See Less

Problem 13

Correct Answer	329
Provided Answer	452
See Solution
% of Participants Solved this	14%
Time Spent (min.)	1

See Less

Problem 14

Correct Answer	116
Provided Answer	54
See Solution
% of Participants Solved this	12%
Time Spent (min.)	2

See Less

View All Questions

PREVIOUS NEXT

MISTAKE ANALYSIS

A summary of the types of mistakes made by the participant and recommendations for improvement.

Problem Number	Correct Answer	Provided Answer	Observations
8	52	7	Luke's answer demonstrates that he was able to cross-multiply to solve a proportion. Most likely, he multiplied by "12" instead of "1.2" at first, which indicates that Luke either omitted the decimal point while working through the calculations or did not correctly place the decimal point after the multiplication. We recommend working with Luke on paying attention to detail when he reads, plays, and listens, and we recommend more practice with decimals.
10	13	41	Luke's answer demonstrates that he understood and correctly performed almost every step of this difficult problem. However, Luke most likely misinterpreted the "3/4 of an ounce from the second bowl" to mean "3/4 of the second bowl." We recommend working with Luke on paying attention to detail when he reads, plays, and listens.

Problem 8

Correct Answer	52
Provided Answer	7
Observations: Luke's answer demonstrates that he was able to cross-multiply to solve a proportion. Most likely, he multiplied by "12" instead of "1.2" at first, which indicates that Luke either omitted the decimal point while working through the calculations or did not correctly place the decimal point after the multiplication. We recommend working with Luke on paying attention to detail when he reads, plays, and listens, and we recommend more practice with decimals.

See Less

Problem 10

Correct Answer	13
Provided Answer	41
Observations: Luke's answer demonstrates that he understood and correctly performed almost every step of this difficult problem. However, Luke most likely misinterpreted the "3/4 of an ounce from the second bowl" to mean "3/4 of the second bowl." We recommend working with Luke on paying attention to detail when he reads, plays, and listens.

See Less

PREVIOUS NEXT

QUESTIONS & SOLUTIONS

Below is a full list of the 2025 International Math Contest questions and the solution to each question.

Question 1:

Find x, if

Solution:

Using the cross-multiplication property of proportions, we create a new equation:

28·3=2·x. After solving this equation, we get: x=42.

See Solution See Less

Question 2:

Tom is 40 inches tall. The sign next to the Superman Roller Coaster says: “You must be 48 inches to ride!”. By what percent does Tom have to grow to be able to ride the roller coaster?

Solution:

If Tom is 40 inches tall now and he must be 48 inches tall, he has to grow by 8 inches. So, he needs to grow by

of his current height, or 20%.

See Solution See Less

Question 3:

Evaluate: 64+

·(−27)

Solution:

Following the order of operations, we must first perform multiplication and then addition. Thus

⋅ (−27)=−3,

64+(−3)=61.

See Solution See Less

Question 4:

A turtle participates in a 40 meter race. She crawled 30 meters in 48 minutes. If the turtle crawled the entire race at the same speed, how many minutes did it take?

Solution:

We know that the turtle crawled 30 out of 40 meters (

of the race) in 48 minutes. Dividing 48 by 3, we find that it crawled

of the race in 16 minutes. Therefore, it took 16 ⋅ 4=64 minutes to finish the race.

See Solution See Less

Question 5:

Emily is playing a game where she receives 2 points as soon as she solves three puzzles correctly. For every ten correctly solved puzzles, Emily earns 3 additional points. How many points did Emily receive if she solved 30 puzzles in all?

Solution:

If Emily earns 2 points for every three puzzles she correctly solves, she will earn 30÷3 ⋅ 2=20 regular points. Since she earns 3 additional points for every ten puzzles, she will also earn 30÷10 ⋅ 3=9 additional points. Her final score is 20+9=29 points.

See Solution See Less

Question 6:

The top of a square table is covered with four equal square tiles. If the side length of each tile is decreased by 50%, how many tiles of the new size would be needed to cover the same table?

Solution:

When the side length of a tile decreases by 50%, it becomes half of its original length. So, each original tile can be covered by four new small tiles, as shown in the picture. Since there are 4 original tiles on the table, we need 4·4=16 new small tiles.

See Solution See Less

Question 7:

Before hosting their annual Chess Tournament and Spelling Bee, a school received 7 boxes of honorary medals: one medal for every participant. After the Chess Tournament, two boxes were empty and the rest were still closed. After the Spelling Bee, which had twice as many participants, there were 72 medals left. How many people competed in the Chess Tournament?

Solution:

We know that 2 boxes of medals were used up for the Chess Tournament. Since there were twice as many participants in the Spelling Bee, it follows that twice as many boxes were used, therefore 4 boxes were used for the Spelling Bee. That makes a total of 6 boxes used. Since there were 7 boxes total, and there are 72 medals left after 6 boxes were used, there must be 72 medals in the last box (and in each box). If there are 72 medals per box and 2 boxes were used for the Chess Tournament, there were 144 participants in the Chess Tournament.

See Solution See Less

Question 8:

Find x, if

0.6−0.3x

=−

1.2

Solution:

Using the cross-multiplication property of proportions, we create a new equation:

1.2(0.6−0.3x)=−18·1.

Then, 0.72−0.36x=−18,

−0.36x=−18.72,

x=52.

See Solution See Less

Question 9:

Dana sent her mom 60 texts in July, which is 60% fewer texts than her mom sent Dana that month. How many total texts did they exchange in July?

Solution:

Let the number of texts that Dana's mom sent be x. According to the problem, 60 is 60% less than x. We can express 60% as the decimal 0.6, so 60% of x is 0.6x and therefore "60% less than x" is x−0.6x=0.4x. Since 0.4x=60 texts, we can divide both sides by 0.4 to get that x=150. Finally, if the number of texts Dana's mom sent is 150 and Dana sent 60, the total number of texts they sent is 150+60=210.

See Solution See Less

Question 10:

A witch made two bowls of potion. The first bowl contains 28.5 ounces of potion, and the second bowl contains 3 ounces of potion. She poured

ounces from the second bowl into the first one. How many times as much potion is in the first bowl as in the second bowl?

Solution:

The amount of potion in the first bowl increases by

of an ounce or 0.75, so 28.5+0.75=29.25. The amount of potion in the second bowl decreases by 0.75, so 3−0.75=2.25. So, the witch has 29.25÷2.25=13 times as much potion in the first bowl as in the second bowl.

See Solution See Less

Question 11:

The measures of the angles of a triangle are in the ratio 2:3:4. The simplified ratio of the measures of the exterior angles of the triangle is a:b:c. Find a+b+c.

Solution:

The measure of an exterior angle of a triangle is equal to the sum of the two opposite (non-adjacent) interior angles of the triangle. If the interior angles of the triangle are in the ratio 2:3:4, the measures of the exterior angles would be 2x+3x=5x; 3x+4x=7x; and 2x+4x=6x. Therefore, the ratio of the exterior angles a:b:c would be 7:6:5 and the sum a+b+c = 7+6+5=18.

See Solution See Less

Question 12:

Mia and Luke made 85 origami together. Mia made 4 pieces of origami every 3 minutes. Luke made 3 pieces of origami every 4 minutes, but Luke spent 5 minutes more than Mia. How many pieces of origami did Mia make?

Solution:

We know that Mia made 4 pieces of origami every 3 minutes, so Mia's rate was

pieces of origami per minute. Luke's rate was

pieces of origami per minute.

Let t minutes be the time that Mia spent making the origami. Then, (t+5) minutes is the time that Luke spent making the origami.

The total number of origami pieces that Mia made is

·t, and the total number of origami pieces that Luke made is

(t+5).

We know that

(t+5)=85.

Solving this equation, we get:

16t+9t+45=1020,

25t=975,

t=39.

Then, we can find the total number of origami pieces that Mia made:

·39=52 pieces of origami.

See Solution See Less

Question 13:

The Charleston family has less than 500 Dalmatians. There are six times as many Dalmatians with black spots on their right ears as Dalmatians without these spots. After giving away 6% of their Dalmatians, how many do the Charlestons have left?

Solution:

Let x be the number of Dalmatians without black spots on their right ears. Then, 6·x is the number of Dalmatians with black spots on their right ears, and then x+6·x=7·x is the number of all the Dalmatians.

Thus, we know that the number of all the Dalmatians must be divisible by 7.

Also, we notice that the Charlestons gave away 6% of all their Dalmatians and we can see that 6% of a number is

100

of the number. Thus, the number of all the Dalmatians must be divisible by 50.

Taking both divisibility conditions into account, we find that the number of all Dalmatians is divisible by 7·50=350, which gives us 350 Dalmatians in total.

Since they gave away 6% of the Dalmatians, we can find 6% (or

) of 350 which is equal to 21. Finally, 350−21=329 Dalmatians left.

See Solution See Less

Question 14:

A blogger who is just starting out made three videos. So far, she has 312 subscribers, who watched one, two, or all three videos. The three videos got 740 total views all together. Assuming each subscriber only viewed a particular video once, how many more people watched all three videos than only one video?

Solution:

Let x be the number of subscribers who watched only one video, let y be the number of subscribers who watched two videos, and let z be the number of subscribers who watched all three videos. Then, x+y+z=312.

Also, 1·x is the number of views made by the subscribers who watched only one video, 2·y is the number of views made by the subscribers who watched two videos, and 3·z is the number of views made by the subscribers who watched all three videos. Then, x+2y+3z=740.

Now we multiply the first equation by 2 and get 2x+2y+2z=624. Then we subtract this equation from the equation x+2y+3z=740, and we get z−x=116. This means that 116 more people watched all three videos than only one video.

See Solution See Less

Problem Number	Correct Answer	Provided Answer	% of Participants Solved this	Time Spent (min.)
1	42	42	94%	0.5
2	20	20	67%	0.5
3	61	61	83%	0.5
4	64	64	84%	1
5	29	29	70%	1
6	16	16	44%	1
7	144	144	51%	1
8	52	7	39%	3
9	210	210	37%	6
10	13	41	42%	3
11	18	18	15%	2
12	52	42	22%	9
13	329	452	14%	1
14	116	54	12%	2

Problem Number	Correct Answer	Provided Answer	% of Participants Solved this	Time Spent (min.)
1	42	42	94%	0.5
2	20	20	67%	0.5
3	61	61	83%	0.5
4	64	64	84%	1
5	29	29	70%	1
6	16	16	44%	1
7	144	144	51%	1
8	52	7	39%	3
9	210	210	37%	6
10	13	41	42%	3
11	18	18	15%	2
12	52	42	22%	9
13	329	452	14%	1
14	116	54	12%	2

Problem Number	Correct Answer	Provided Answer	% of Participants Solved this	Time Spent (min.)
1	42	42	94%	0.5
2	20	20	67%	0.5
3	61	61	83%	0.5
4	64	64	84%	1
5	29	29	70%	1
6	16	16	44%	1
7	144	144	51%	1
8	52	7	39%	3
9	210	210	37%	6
10	13	41	42%	3
11	18	18	15%	2
12	52	42	22%	9
13	329	452	14%	1
14	116	54	12%	2